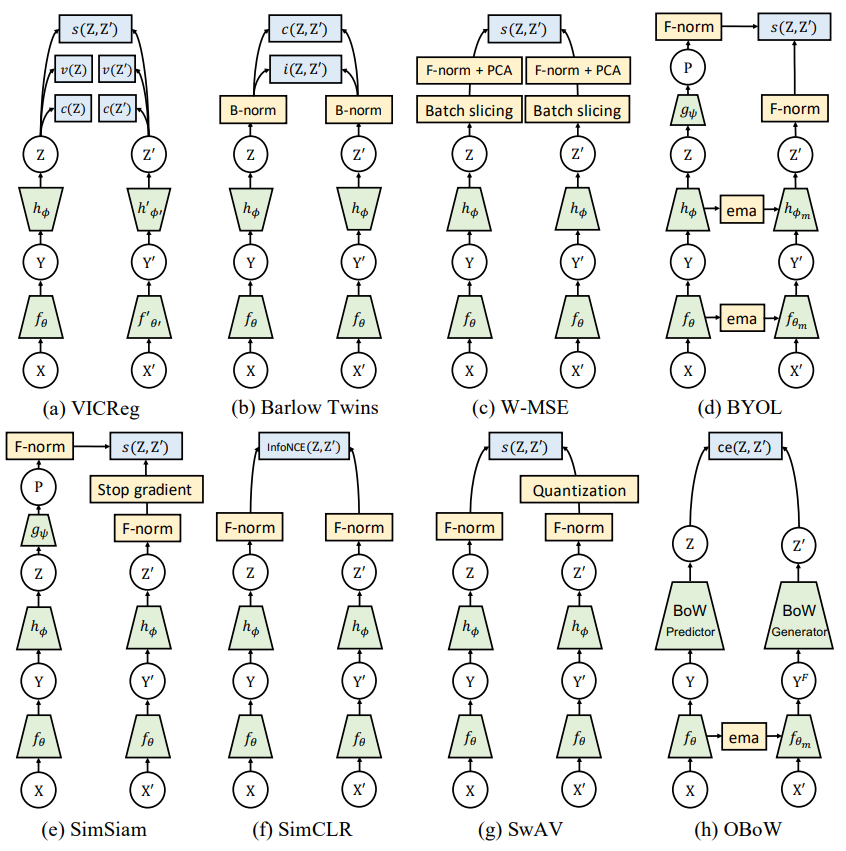
这篇文章主要是在loss上进行改进,不使用infoNCE进行对比学习。
假设有两个batch,一个是weak aug经过网络得到的feature $Z=[z_1,z_2,\dots,z_n]$,一个是经过strong aug之后经过网络得到的feature $Z^\prime=[z_1^\prime, z_2^\prime, \dots, z_n^\prime]$。
variance regularization
\[v(Z)=\frac 1d\sum_{j=1}^d \max(0,\gamma-S(z^j,\epsilon)),\ S(x,\epsilon)=\sqrt{Var(x)+\epsilon}\tag1\]$d$是dimension(维度),$\gamma$是一个常数,实验中fix到1,在每一个维度上做hinge loss。作者称之为variance regularization。直观上,这一项希望一个batch内feature的方差在每一个dimension为$\gamma$,这样就可以保证模型不会将所有的输入都映射到一个点,防止了坍塌。
covariance regularization
作者这里借鉴了Barlow Twins的想法,设计了如下loss \(C(Z)=\frac 1{n-1}\sum_{i=1}^n (z_i-\bar z)(z_i-\bar z)^T, \bar z=\frac 1n\sum_{i=1}^n z_i\tag2\)
\[c(Z)=\frac 1d \sum_{i\neq j}[C(Z)]^2_{i,j}\tag3\]在batch的维度上先白化(减$\bar z$),再求feature之间的相关性,实际上$C(Z)$是一个$d\times d$的矩阵。那么$c(Z)$的目标是想让$C(Z)$为单位阵。也就是说,希望每个维度之间不相关,防止他们维度之间过于相似(decorrelate)。
MSE loss
还有一项就是两个增强后的图像得到的feature应该相近,作者这里直接使用了MSE loss。 \(s(Z,Z^\prime)=\frac 1n \sum_i \|z_i-z_i^\prime\|_2^2\)
伪代码

