推断问题分为精确推断和近似推断，而近似推断又分为确定性（VI）和随机（MCMC）两者。本文介绍是MCMC（markov chain & monte carlo），基于采样的随机近似方法。

问题引入

假设我们有以下后验，$p(z\mid x)$，$x$表示可观测数据，$z$表示隐变量。

假设我们需要计算在该后验概率下的$f(x)$的期望$\mathbb E_{z\mid x} [f(z)]=\int p(z\mid x) f(z) dz$，我们可以将其近似为求和的形式$\mathbb E_{z\mid x} [f(z)]\approx\frac 1N \sum f(z_i), \exists z^{(1)},z^{(2)},\cdots, z^{(n)}\sim p(z\mid x)$，这样我们就可以近似求出该期望了。

但是对于大多数后验概率来说，对其采样的难度很大。因此引入下面的方法进行采样。

概率分布采样

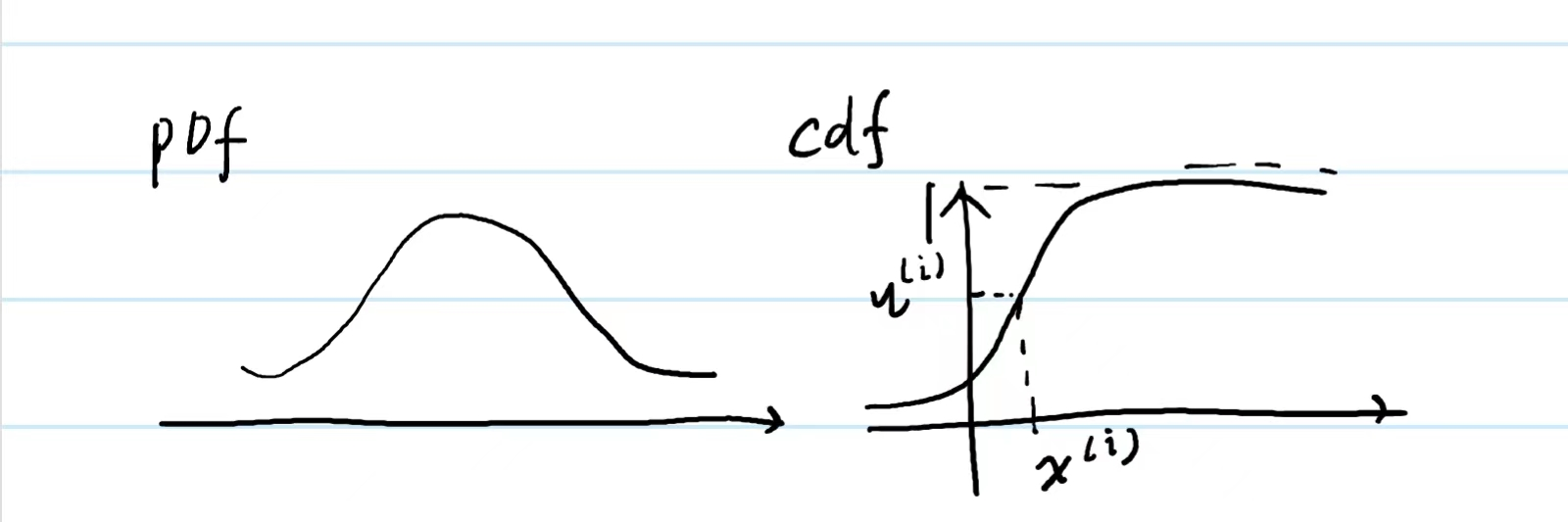
我们可以从简单的均匀分布中采样$\mu\sim U(0,1)$，对于每一个$\mu^{(i)}$，可以求得相应的$x^{(i)}=cdf^{-1} (\mu^{(i)})$

弊端有： 当pdf很复杂的时候，可能求不出cdf

拒绝采样

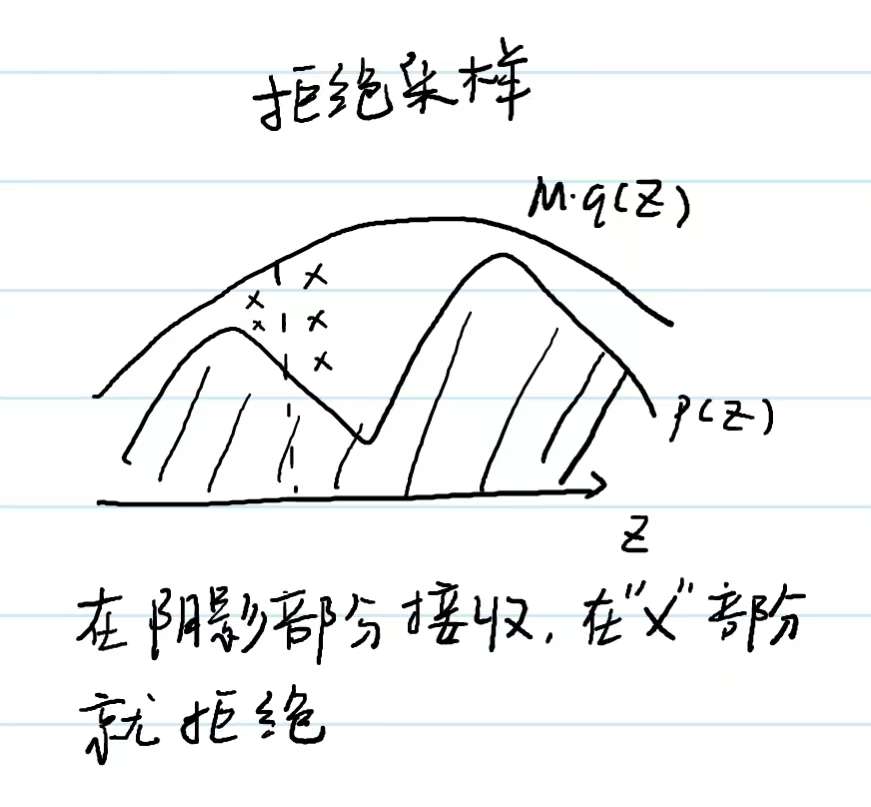
引入一个提议分布$q(z)$（proposed distribution）,$\forall z_i, Mq(z_i)\geq p(z_i)$，要保证$M(q(z_i))$处处大于$p(z)$。

我们先引入一个概念，接受率$\alpha=\cfrac{p(z^{(i)})}{Mq(z^{(i)})}, 0\leq \alpha\leq 1$，采样方式如下：

1. 先从$q(z)$中采样一个$z^{(i)}$
2. 从均匀分布取出$\mu \sim U(0,1)$
3. 如果$\mu \leq \alpha$，接收$z^{(i)}$，否则拒绝。

当$Mq(z)$与$p(z)$越接近，接受率越高，问题是我们根本就不知道$p(z)$的形状，自然也不能保证接受率。

重要性采样

并不是直接对$p(z)$，而是对$p(z)$的期望采样，我们仍然可以引入一个提议分布： \(\mathbb E_{p(z)}[f(z)]=\int p(z)f(z)dz=\int \cfrac{p(z)}{q(z)}q(z)f(z)dz\\= \int f(z)\cfrac{p(z)}{q(z)}q(z)dz\approx \cfrac 1N \sum_{i=1}^N f(z_i )\boxed{\cfrac{p(z_i)}{q(z_i)}},\ z_i \sim q(z), i=1,\cdots,N\)

框起来的部分叫做weight。

问题仍然是严重依赖于$p(z)$与$q(z)$的关系。

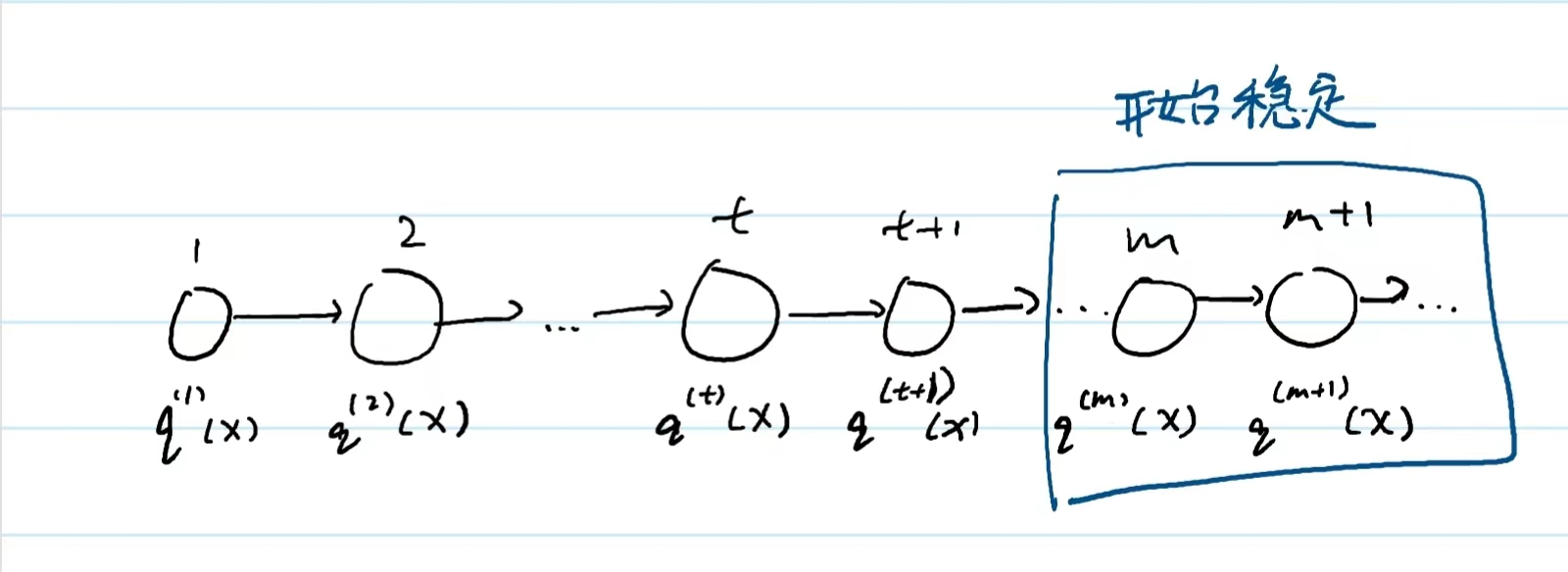
MCMC

思想

MCMC的思想就是建立一个马尔可夫链，使得当链稳定的时候，其稳定概率（平稳分布）$p(x)$就是我们想要的采样的后验概率。